In this lesson, we define what a parameter is and how to compute the number of such parameters in each layer using a simple convolutional neural network.
Which parameters are examined?
Stochastic Gradient Descent (SGD) is used to learn and optimize weights and neural network biases during training. These weights and biases are really learnable parameters. In fact, all parameters in our model that are learned by the DMS are considered as learnable parameters. These parameters are also called trainable because they are optimized in the training process.
Make the model
Here we build a simple CNN model for image classification with an input layer, three hidden convolution layers and a dense output layer.
def create_model() :
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(kernel_size=(3,3), filters=32, padding= ‘same’, activation= ‘relu’, input_shape=[img_SIZE,img_SIZE,3],name=Conv1)
tf.keras.layers.Conv2D(kernel_size=(3,3), filters=64, padding=’same’, activation=’relu’,name=Conv2,use_bias=True),
tf.keras.layers.MaxPooling2D(pool_size=2,name=Max1),
tf.keras.layers.Conv2D(kernel_size=(3,3), filters=128, padding= ‘same’, activation= ‘relu’,name=Conv3),
tf.keras.layers.Conv2D(kernel_size=(1,1), filters=256, padding= ‘same’, activation= ‘relu’,name=Conv4),
tf.keras.layers.GlobalAveragePooling2D(name=GAP1),
tf.keras.layers.Dense(10,’relu’,name=Dense1),
tf.keras.layers.Dense(10,’softmax’,name=Output)]
model.compile(optimizer=tf.keras.optimizers.RMSprop(),
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()])
return model
model=create_model()
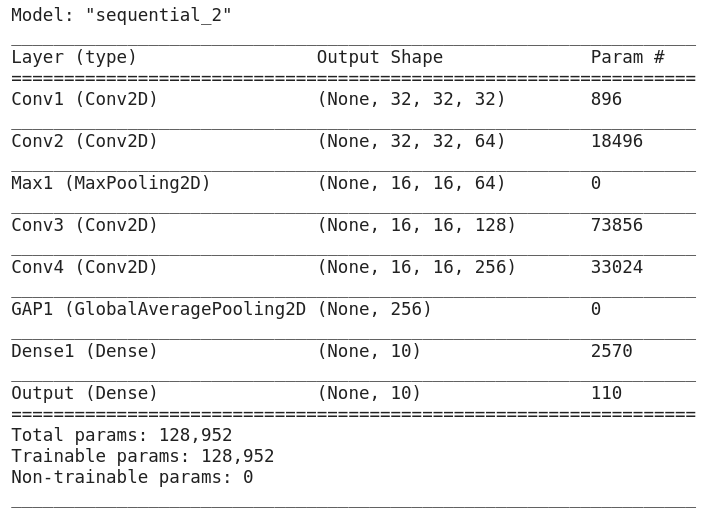
model.summary()
Our input layer consists of 32x32x3 image input, where 32×32 defines the width and height of the images and 3 defines the number of channels. The three channels indicate that our images are in the RGB color space, and these three channels represent the input features in this layer.
Our first convolutional layer consists of 32 3×3 filters. Our second convolutional layer consists of 64 3×3 filters. And our exit layer is a dense layer at 10 knots.
Preload
First, we need to understand whether or not the layer contains an offset for each layer. If that is the case, then we are only increasing the level of bias. The number of offsets is equal to the number of nodes (filters) in the layer. Moreover, we assume that our network is biased. This means that there are terms of bias in our hidden and output layers.
Parameters for input layer
The input layer has no parameters that can be examined, since the input layer consists only of input data and the output data of the layer is actually only treated as input data for the next layer.

Convolution layer parameter
The convolutional layer contains filters, also called nuclei. We must first determine how many filters are in the convolutional layer and how large they are. We must include these elements in our calculations.
The input for the convolution layer depends on the previous layer types. If it was a dense layer, it’s just the number of nodes in the previous dense layer.
If it was a convolutional layer, the input is the number of filters of the previous convolutional layer.
At the output of the convolution layer, the number of filters is multiplied by the filter size. With a dense layer, it was just the number of branches.
Let us calculate the number of studied parameters in the convolutional layer.
Convolution layer 1
tf.keras.layers.Conv2D(kernel_size=(3,3), filters=32, padding=’same’, activation=’relu’, input_shape=[IMG_SIZE,IMG_SIZE,3],name=Conv1)
We have three input signals from our input layer. The number of outputs is the number of filters multiplied by the filter size. So we have 32 filters, each of 3×3 size. So, 32*3*3 = 288. If we multiply our three inputs by 288 outputs, we get 864 weights. What is the extent of the prejudice? There are 32 in total, since the number of offsets equals the number of filters. Thus, we obtain 896 common study parameters in this layer.
Convolution layer 2
tf.keras.layers.Conv2D(kernel_size=(3,3), filters=64, padding=’same’, activation=’relu’,name=Conv2,use_bias=True)
Let’s go to the next convolutional layer. How many inputs come from the previous level? We have 32, which is the number of filters from the previous layer. How many exits? Well, we have 64 filters, always 3×3. That makes 64*3*3 = 576 outputs. Multiplying our 32 inputs from the previous layer by 576 outputs, we have 18432 weights in this layer. Adding the offset conditions of the 64 filters gives 18496 digestible parameters at this level.
Then we perform the same calculation for the other layers of the network
dense layer
For a dense layer, this is indicated by the number of parameters examined:
Inputs * Outputs + Offsets
In general, the number of parameters to be examined in the computed layer is the number of inputs multiplied by the number of outputs plus the number of offsets.
This gives us the number of digestible parameters in a given layer. You can add up all the results to get the total number of parameters examined for the entire network.
Related Tags:
how to calculate parameters in keras model, convolution and fully connected layers contain parameters, pooling does not., how to count number of parameters in a model, calculate number of parameters in fully connected neural network, bidirectional rnn number of parameters, keras model summary, number of parameters in embedding layer, convolutional neural network



